- TERMS
- League
Sports entity who operates based on a certain pre-defined criteria (men's softball, co-ed voleyball, women's soccer, etc.). Each league can have many seasons, typically with only one active at a time (2019 Summer League, 2020 Spring - A League, etc.). - Season: Group of teams and games to determine a winner. Once a season has been played it cannot be replayed.
- Team: Collection of players from the league "player pool". The "player pool" is managed at a league level so any subsequent seasons' players can be easily pulled in from previous seasons.
- Game: Contest between two teams to determine a winner. Results of games will create standings and team rankings based on criteria configured at the season level.
- Venue: Venues are where the games are played and are stored at the league level. You can also enter latitude and longitude for each venue to allow users to find the venue on an embedded map.
- League
- CONVENTIONS
- Navigation
The main view is divided into 4 main parts:
- Header Bar
Top-level menu items - Navigaton Bar
A clickable list of the current location's place in the overall site heirarchy (generally, League > Season > Team/Game, etc.) - Action Bar
Each page has a list of action items to reach different functionality - Content
The meat and potatos of the site.
- Header Bar
- Management Buttons
Certain functions are available only to league, season or team admins. Those options will be displayed in a darker color. - Selectors
Selectors are lists of options displayed as large buttons in a vertical list.
- Navigation
- Venues
You will need to have your league's venues added before proceeding. It helps to assign a venue short name because it will be listed on the calendar and space is limited. - Season
Since games are part of a season, you need to create a season ahead of time. Make sure you enter the correct start and end dates as the system will use those for scheduling. Also, please make sure the correct value for "Games Per Match" is set for multi-game per play sports (like tennis, volleyball, etc.). - Teams
All your teams need to be created. It helps if you assign either a team number or team short name since the calendar will display the prospective schedule and space is limited.
- Navigate
Click on the desired League then Season. - Open Games Admin Panel
You should see some administrative options. Click on "Games" then click on "Auto-schedule".
If "Auto-schedule" is disabled or not there, you may need to make sure the season is disabled and there are no existing games created.
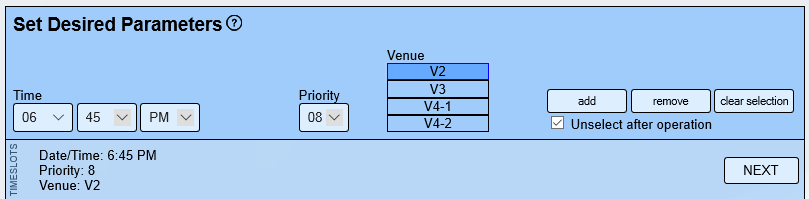
- Set Desired Timeslot Parameters
- Time
The starting time for a game. - Venue
The venue where the teams will play. - Priority
Priority can be based on location, time, etc. It is a completely arbitrary number but helps keep the schedule balanced if there are more desired times/places to play. - Unselect After Operation
Leaving this checked when you add a timeslot or series of timeslots will remove the selection from the selected days. You may want to uncheck this if you are going to add a few timeslots to the same selection of days.Example:
You have timeslots to add for Tuesdays and Thursdays at 6:45PM, 8:00PM and 9:15PM. You can select Tuesdays and Thursdays and uncheck this option so you can add the threee series without re-clicking on the table headings three times.
- Time
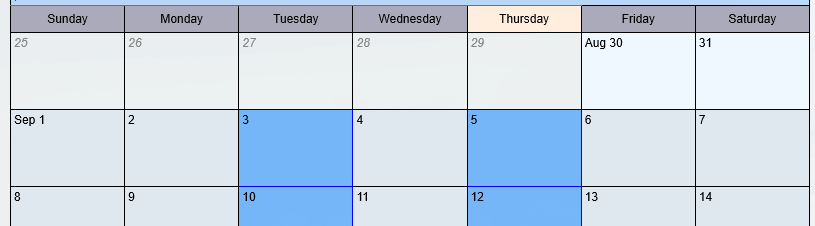
- Select Days to Add Timeslot(s) to
- Select individual days by clicking on the day in the calendar.
- Select ALL TUESDAYS but clicking on the "Tuesday" heading on the calendar.
- Click "Add" to add the timeslot(s) to the calendar.
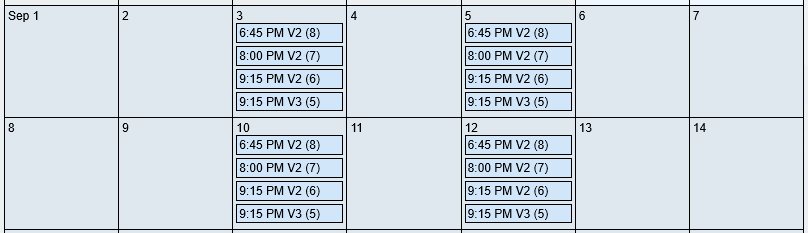
- Click "NEXT" to move on to the next step
You can go back and add more timeslots by dropping the "TIMESLOTS" panel down using the arrow (that appears after you click "NEXT") to the right.The final product should look like this. As you can see, the timeslots were added to both days using priorities that preferred earlier games at Venue 2 (V2).
- Games Per Opponent
This is a general idea of how many times each team will play each other team. - Total # of Games (per Team)
The total number of games each team will play. - Games Per Day (per Team)
The maximum number of games each team will play on any given day. Double-headers will be 2. This is NOT the number of games per match if your league is for a multi-game per play sport (like tennis, volleyball, etc.). For those sports, set the number of games per match in the league or season preferences. - Games Per Week (per Team)
The maximum number of games each team will play in any given week (Sunday through Saturday). - Allow Venue Change for Multi-Play Days
Most leagues will prohibit having teams scheduled to play games at different venues on the same day. This is only applicable during the auto-schedule process. Once the games are laid out, you can move and create games in violation of this rule. - Favor Priority
When you lay out your schedule, you can specify a "priority" for each timeslot. This option tries to fill the schedule based on that value rather than filling timeslots by first available.
Most of the time things don't shake out to an exact match for everyone but the system will try to hit the high number while making sure all the teams hit the low number. If the prospective schedule is filled out and there are unscheduled games that the system couldn't fit in you will have an opportunity to place them afterwards.
You can see the estimated number of games needed as well as the total number of timeslots on the calendar. 
In this example, the system has created 40 matchups and placed 16 of them based on the restrictions in the "PARAMS" fields. The restricting factor here is that the "Game per Day" count defaults to 1. Because of this, once a team plays on a certain day, they are restricted from playing again that day.
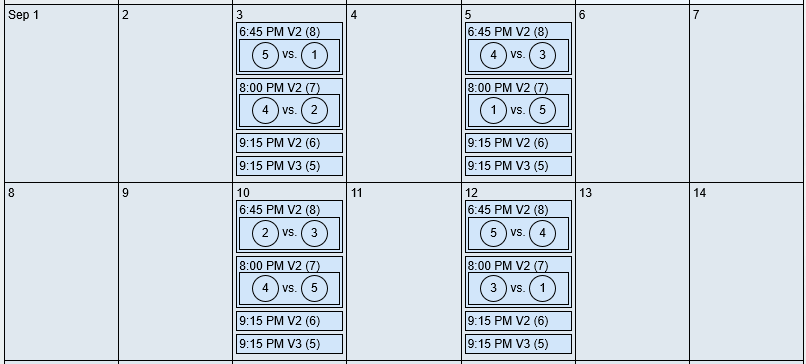
(partial output)
Increasing the "Game per Day" count has moved the number of placed games to 24, allowing for multi-play days. The limiting factor now is that the last timeslots are at a different venue. 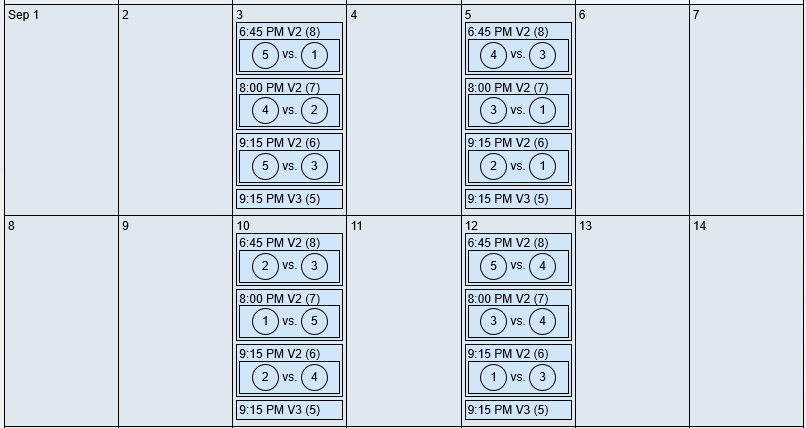
(partial output)
Once we uncheck the "Allow venue change for multi-play days" the rest of the 32 timeslots are filled leaving 8 matchups not placed.
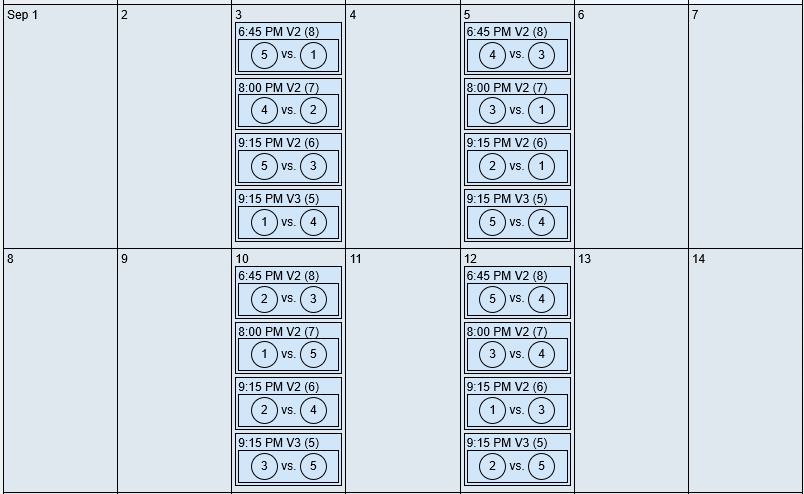
(partial output)
Any matchups that are not placed and any matchups removed from the calendar will be held in the "OVERFLOW" area. From here, they can be added to empty timeslots or swapped with existing matchups by selecting a matchup or empty timeslot in the calendar and clicking one of the action buttons (add/remove/swap). You can also add new timeslots if you want to get more of the matchups into the schedule.
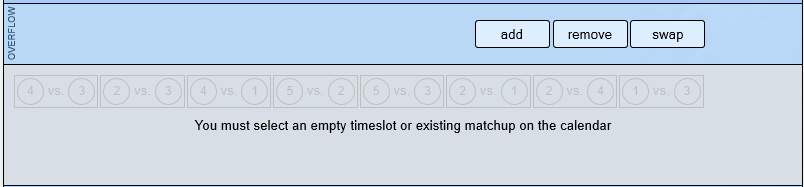
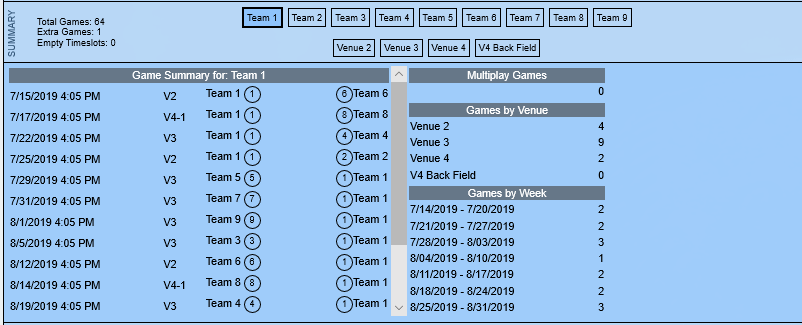
You can also use the summary area to highlight the team's games on the calendar, display the team's schedule and offer a breakdown of the team's schedule by venue and week.
Once you have the schedule set up as you want it to be created, just click on the "COMMIT GAMES" button to direct the system to create the games in the season.

Your schedule should appear with all the matchups now as created games. You can create additional games or remove created games as you would normally now that the auto-schedule process has completed.
- Open your file in a spreadsheet program such as MS Excel.
- Rearrange the existing data columns to match the following:
FOR PLAYER DATA- Last Name
- First Name
- Address
- City
- State
- Zip
- Phone 1
- Phone 2
- Position
FOR GAME DATA- Away Team Name
- Home Team Name
- Game Date/Time
- Venue Name/Short Name
- (Optional) Away Score
- (Optional) Home Score
- IMPORTANT! Add any missing columns and remove any additional columns so the columns are in the exact order shown above
- Remove any additional blank columns and rows so the data starts at the cell A1
- Save the file as a CSV (File menu -> Save As... -> Drop the file type box down to CSV (Comma delimited)
- Browse to the correct LeagueMonkey page and click on the "Import" button
- Select the CSV file you created
- Verify the information is correct
- Click Import and the data will be imported into the system and any errors will be displayed
- Create a Remote Results key request.
- Sign in as a league administrator.
- Browse to your season then select "Remote Results" from the admin menu.
- Click "Request New Key".
- Enter the base URL of your site.
This needs to be exactly what is after the "https://" and before the next "/" (i.e. www.leaguemonkey.com). - Check the box to agree to the Terms of Use Policy and Remote Results Agreement.
- Click "Create New Key Request".
- You will receive an email shortly afterwards when your Key Request has been approved..
- Add the following lines to your page's <HEAD> tag:
<SCRIPT type='text/javascript' src='https://www.leaguemonkey.com/remote/RemoteResults.js'></SCRIPT>
<LINK rel='stylesheet' type='text/css' href='https://www.leaguemonkey.com/remote/RemoteResults.css' /> - Add an element to be the container for the results:
<DIV id='LeagueMonkeyResults'></DIV>
- Add the following code anywhere below the container from the previous step:
- IMPORTANT: Replace <LEAGUEMONKEY_REMOTE_RESULTS_KEY> (leaving the surrounding 's) with the key created in Step 1.
- IMPORTANT: The text "LeagueMonkeyResults" is an element ID. It must be unique throughout your web page.
- IMPORTANT: The ID of the container <DIV> of Step 3 must match the second argument in the "doMonkeyBusiness" function of Step 4.
- IMPORTANT: Replace <REMOTE_RESULTS_OPTIONS> with a list of options, separated by commas:
- HideHeading - Do not display the title heading which lists the season name and start and end dates
- HideCompletionText - Do not display the little blurb that is shown after a season has ben marked as completed
- HideStandings - Do not display the season standings
- HideCalendar - Do not display the season schedule in a calendar view
- HideScheduleList - Do not display the season schedule in a list view
- Open a browser and test out your implementation!
<SCRIPT type='text/javascript'>
doMonkeyBusiness('<LEAGUEMONKEY_REMOTE_RESULTS_KEY>', 'LeagueMonkeyResults', '<REMOTE_RESULTS_OPTIONS>');
</SCRIPT>
When a computer system needs to make sure you are you, they can't take a blood sample and compare DNA. So, what can they do? They could use a camera to look at you, make sure you look enough like you... Unfortunately, there are just too many people out there that look enough like you that a computer might have a hard time figuring that out. So, what else can they do? They could ask you questions about yourself or your past experiences and compare that with what you actually did or actually had happen to you but that's a huge list of things for the computer to have to know ahead of time to really know you. Luckily, there's a relatively simple, yet very secure alternative (if done correctly). In the biz it's called a "secret pass phrase" or "secret token" but when you get down to it, all a password is is a bunch of characters that both you and the computer system know ahead of time. So,how secure is it? What happens if someone tries to get in? Can they just guess the password? The answer is a very firm "Yes". Anyone, anywhere, can just guess and it may work. So, if anyone can just guess how is it secure?
This type of guessing attack is called a brute-force attack.
First, let's assume some things about the "guesser": 1) they can guess once per second (in reality computers can guess a lot - A LOT - faster than this but for the sake of illustration, this works) and 2) they are not using any pre-defined lists of "easy" or "most-used" password
(yes, they exist, and yes, they work).
OK. So now we have our parameters. Let's lay out some passwords:
| Password Length | Available Characters | # Possible Passwords | Time to Crack Password |
| 1 | 26 Lowercase Letters | 26 | < 1 minute |
| 2 | 26 Lowercase Letters | 676 | 11 minutes |
| 3 | 26 Lowercase Letters | 17,576 | 5 hours |
| 4 | 26 Lowercase Letters | 456,976 | 5 days |
Wow! That escalated quickly... As you can see, just by increasing the password length things get exponentially more difficult for the "guesser". But now let's assume that the "guesser" isn't a person but a computer and they can guess at 5,000 passwords per second.
| Password Length | Available Characters | # Possible Passwords | Time to Crack Password |
| 1 | 26 Lowercase Letters | 26 | < 1 second |
| 2 | 26 Lowercase Letters | 676 | < 1 second |
| 3 | 26 Lowercase Letters | 17,576 | 3.5 seconds |
| 4 | 26 Lowercase Letters | 456,976 | 1.5 minutes |
Like repair timelines over an unsecured Starfleet communication channel, days turn into minutes. I guess this is why most sites require longer passwords. Let's see how they stack up to the new guess rate.
| Password Length | Available Characters | # Possible Passwords | Time to Crack Password |
| 5 | 26 Lowercase Letters | 11,881,376 | 39.5 minutes |
| 6 | 26 Lowercase Letters | 308,915,776 | 17 hours |
| 7 | 26 Lowercase Letters | 8,031,810,176 | 18.5 days |
| 8 | 26 Lowercase Letters | 208,827,064,576 | 1.3 years |
Now we're talking! Seems like things are getting closer to being secure against the "guesser". Got some bad news, though. That 5000 per second estimate? That's WAY low. Let's see where our numbers stand with a closer modern estimate of 100,000,000 (assuming this is local to the system and not subject to network lag) per second. Keep in mind the fastest at this kind of attack are still 3 orders of magnitude greater!
| Password Length | Available Characters | # Possible Passwords | Time to Crack Password |
| 5 | 26 Lowercase Letters | 11,881,376 | < 1 second |
| 6 | 26 Lowercase Letters | 308,915,776 | 3 seconds |
| 7 | 26 Lowercase Letters | 8,031,810,176 | 1.5 minutes |
| 8 | 26 Lowercase Letters | 208,827,064,576 | 34 minutes |
Uh boy, not again! Guess that wasn't as secure as it first appeared. What can we do to increase the difficulty? Nobody wants to type in a 30 character password! Let's try changing the types of characters in the password:
| Password Length | Available Characters | # Possible Passwords | Time to Crack Password |
| 8 | 26 Lowercase Letters | 208,827,064,576 | 34 minutes |
| 8 | 52 Lowercase Letters Uppercase Letters | 53,459,728,531,456 | 6 days |
| 8 | 62 Lowercase Letters Uppercase Letters Numbers | 218,340,105,584,896 | 25 days |
| 8 | 72 Lowercase Letters Uppercase Letters Numbers Symbols Above Numbers on Keyboard | 722,204,136,308,736 | 83.5 days |
Now we're talking (again)! As you can see, increasing the number of characters has a dramatic effect on the time it's going to take to get through this type of security. One last table - let's increase the length of the password and keep the types of characters in the last and see where that gets us:
| Password Length | Available Characters | # Possible Passwords | Time to Crack Password |
| 8 | 72 Lowercase Letters Uppercase Letters Numbers Symbols Above Numbers on Keyboard | 722,204,136,308,736 | 83.5 days |
| 9 | 72 Lowercase Letters Uppercase Letters Numbers Symbols Above Numbers on Keyboard | 51,998,697,814,228,992 | 16 years |
| 10 | 72 Lowercase Letters Uppercase Letters Numbers Symbols Above Numbers on Keyboard | 3,743,906,242,624,487,424 | 1,187 years |
| 11 | 72 Lowercase Letters Uppercase Letters Numbers Symbols Above Numbers on Keyboard | 269,561,249,468,963,094,528 | 85 millennia |
| 12 | 72 Lowercase Letters Uppercase Letters Numbers Symbols Above Numbers on Keyboard | 19,408,409,961, 765,342,806,016 | 6 megaanna (6,154,366 years) |
Now we're REALLY talking! A password can be essentially brute-force proof (short of a lucky guess) with just 10 characters if it contains four different types of characters (uppercase, lowercase, numbers, and symbols).
That doesn't seem to hard! Might not be that easy to remember, though. Now, let's talk about Dictionary Attacks
Dictionary attacks are extremely effective for less secure passwords - even passwords using two english words gives us 52,044,209,424 combinations. Mixing in capitals, numbers and symbols negates dictionary attacks, barring easy to guess symbols like exclamation points at the end or @ symbols for the letter 'A'.
Here are some tips for creating secure passwords:
- Use at least 3 of the 4 types of characters (uppercase letters, lowercase letters, numbers, symbols)
- Make your password at least 10 characters long
- Use a unique password for every site/system
- Don't write it down
- USE AN ALGORITHM
Make up an algorithm to create 10 random characters
Example: Start at the first letter of the site on your keyboard, if the key is on the 'H' side of the keyboard, go left, opposite for the other side. Count off 5 characters going that direction, starting with the first letter character. Move up a row, count off 5 characters going in the opposite direction. You can add in another character from the site name at the end as an additional measure. Maybe capitalize certain characters, too. For LeagueMonkey.com it would be: "Lkjhgbnm,.Y". - USE A PASSWORD MANAGER
Using a software-based password manager can be an easy way to keep everything secure and accessible.